Asservissement PID - drone ch.8
Sommaire
- 1. Théorie de l'asservissement
- 1.1 Système à boucle ouverte
- 1.2 Système à boucle fermée
- 1.3 Régulateur PID
- 1.3.1 Action Proportionnelle
- 1.3.2 Action Intégrale
- 1.3.3 Action Dérivée
- 1.3.4 Action PID
- 2. Implémentation pour Arduino
- 2.1 Calcul des consignes
- 2.2 Calul des erreurs
- 2.2 Régulateur PID
- 2.3 Start/stop
- 2.4 Compenser la baisse de batterie
- 2.5 Générer les signaux des ESC
- 2.6 Code final
- 3. Cablage
- 4. Calibration des coefficients PID
- 4.1 Banc de test
- 4.2 Procédure de calibration
- 5. Premier vol
- 5.1 Sécurité & législation
- 5.2 Décollage !
- 6. Conclusion
Salut les makers !
Nous voici arrivés au dernier chapitre de cette série d'articles sur la réalisation d'un drone à base d'Arduino.
A ce stade, nous sommes capables de lire les instructions reçues par le récepteur et de lire les mesures angulaires du gyroscope. Nous avons tous les éléments nécessaires pour implémenter notre asservissement.
1. Théorie de l'asservissement
Dans le tout premier chapitre de cette série, nous avons introduit la notion d'asservissement. Nous allons voir plus en détail ce qui ce cache derrière cette notion.
1.1 Système à boucle ouverte
Un système à boucle ouverte ne tient pas compte de la réponse de ce système, c'est-à-dire qu'il n'a pas de boucle de rétroaction (feedback en anglais). Concrètement, ça revient par exemple à conduire une voiture les yeux fermés en espérant que le véhicule va suivre la trajectoire souhaitée.
C'est tout pourri un système à boucle ouverte, à quoi ça peut bien servir ?
La plupart du temps, le contrôle en boucle ouverte est utilisé lorsque la réaction du système est difficile à mesurer ou à diagnostiquer. C'est-à-dire, quand il est très compliqué d'avoir un retour du résultat obtenu.
Ou tout simplement parce que le système ne nécessite pas de boucle de rétroaction. Par exemple, un arrosage automatique n'a pas besoin d'avoir d'information en retour, il se contente d'arroser.
Enfin, l'étude en boucle ouverte permet également de tracer le diagramme de Nyquist d'un système à boucle fermée dans le but d'en étudier sa stabilité.
Ce dernier point est une notion assez avancée d'automatique que nous ne traiterons pas ici.
Dans le cas de notre drone un tel système serait inefficace et l'enverrait dans le décor à coup sûr.
1.2 Système à boucle fermée
Un système est dit à boucle fermée lorsque la sortie du procédé est prise en compte pour calculer l'entrée.
Dans le cadre de notre drene, le système va disposer de capteurs qui donneront des informations sur son état (inclinaison, vitesse angulaire, accélération). Ces dernières seront prises en compte pour corriger la trajectoire du drone.
D'un point de vue schématique, on représente un système à boucle fermée de la manière suivante :
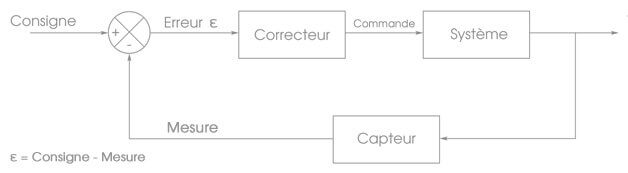
En entrée du système arrive la consigne. C'est l'objectif que l'on donne à notre système (une vitesse, une direction, une température, etc).
À cette consigne on soustrait une mesure effectuée sur le système : on obtient alors l'erreur (notée $\varepsilon$).
Cette erreur est ensuite passée en entrée du correcteur (ou régulateur) qui calcul alors la valeur de sortie du système. Pour nous, la valeur de sortie sera la vitesse de rotation de chaque moteur.
Souvenez-vous, c'est en jouant sur la vitesse de chaque moteur que l'on peut orienter notre drone dans l'espace et lui faire suivre une trajectoire.
1.3 Régulateur PID
Le régulateur (ou correcteur) va appliquer une correction au système en fonction de l'erreur mesurée.
D'un point de vue mathématique, un régulateur PID peut s'exprimer de la façon suivante dans le domaine temporel :
$$u(t) = K_pe(t) + K_i \int_0^t e(t')dt' + K_d \dfrac{de(t)}{dt}$$

Pas de panique, nous allons décortiquer tout ça pour comprendre de quoi il s'agit.
Mais d'abord, ça veut dire quoi PID ?
PID est l'accronyme de Proportionnel, Intégral, Dérivé. Ce sont les trois manières dont le régulateur agit :
- action Proportionnelle : l'erreur est multipliée par un gain $K_p$
- action Intégrale : l'erreur est intégrée et multipliée par un gain $K_i$
- action Dérivée : l'erreur est dérivée et multipliée par un gain $K_d$
Si on reprend le schéma du système à boucle fermée en y intégrant le régulateur PID, voici à quoi ça ressemble :
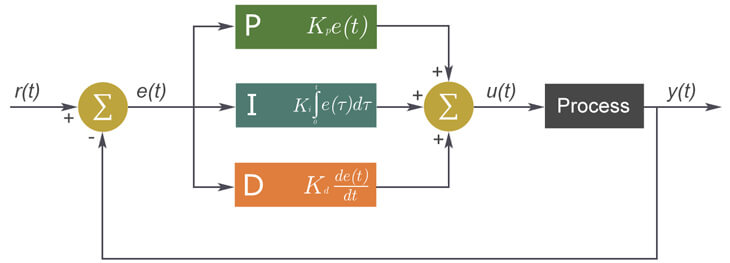
1.3.1 Action Proportionnelle
L'action proportionnelle est la plus intuitive des trois. Il s'agit d'appliquer un coefficient $K_p$ à l'erreur.
$$K_p.e(t)$$
C'est naturellement ce qu'on fait lorsqu'on conduit : lorsque la voiture commence à dévier de sa trajectoire, on donne un coup de volant dans le sens opposé. L'erreur ici est la différence entre la trajectoire souhaitée et celle estimée par nos yeux et la correction apportée est proportionnelle à l'erreur.
Plus on augmente le gain et plus le système réagit rapidement mais il gagne alors en instabilité et perd en précision.
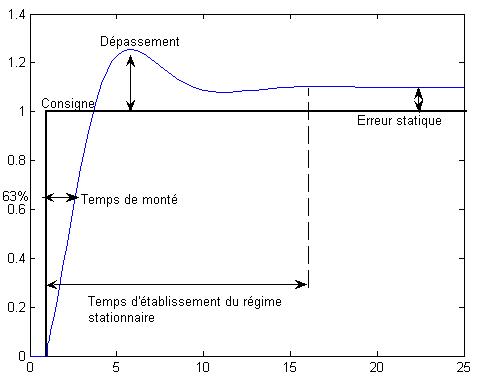
Plus on augmente le gain et plus le système se rapproche de son point d'instabilité. Lorsque ce dernier est atteint, on obtient alors un oscillateur. C'est sur ce principe même que les oscillateurs électroniques fonctionnent.
Lorsqu'on dépasse ce point, le système est alors instable.
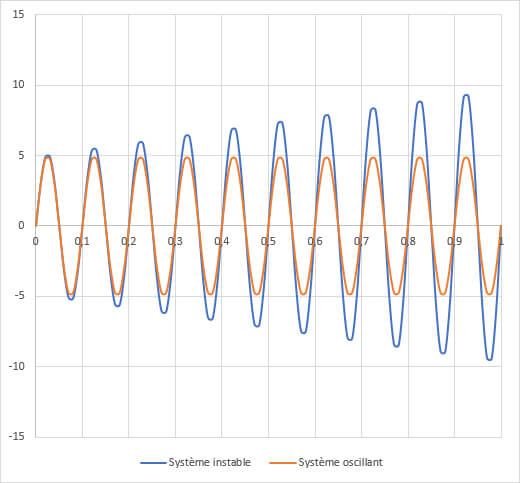
Et on comprend rapidement pourquoi : si je donne un grand coup de volant pour corriger la trajectoire de ma voiture, la correction apportée sera encore pire que l'erreur initiale. La fois d'après ça sera encore pire et ainsi de suite.
| Précision | Stabilité | Rapidité |
|---|---|---|
| ↘ | ↘ | ↗ |
1.3.2 Action Intégrale
L'action intégrale consiste à sommer dans le temps les erreurs mesurées et d'appliquer un coefficient $K_i$ à l'ensemble :
$$K_i \int_0^t e(t')dt'$$
Cette composante permet de réduire l'erreur statique et donc d'améliorer la précision du système. En revanche, elle augmente l'instabilité et diminue la rapidité.
| Précision | Stabilité | Rapidité |
|---|---|---|
| ↗ | ↘ | ↘ |
1.3.3 Action Dérivée
L'action dérivée consiste à calculer la différence entre l'erreur courante et l'erreur à t-1 et d'appliquer un coefficient $K_d$ au résultat :
$$K_d \dfrac{de(t)}{dt}$$
Cette composante augmente la stabilité du système mais au détriment de la rapidité.
| Précision | Stabilité | Rapidité |
|---|---|---|
| - | ↗ | ↘ |
1.3.4 Action PID
Au final, un régulateur PID est un savant mélange de ces trois actions.
Sur l'animation suivante on peut voir les effets de chaque action sur la réponse d'un système à une consigne de type échelon :
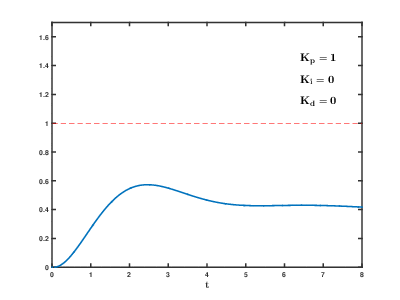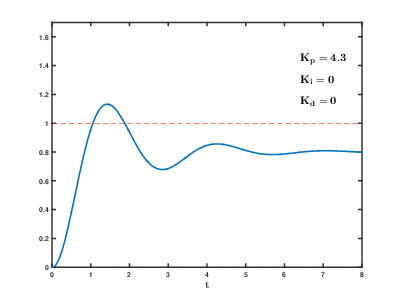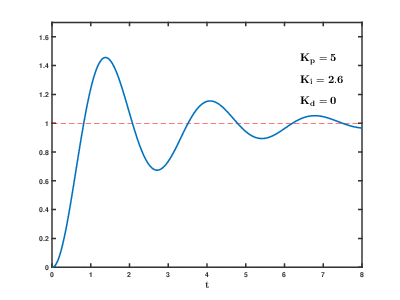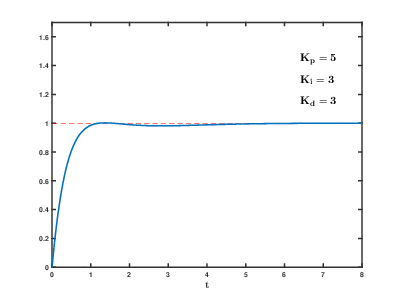
2. Implémentation pour Arduino
Notre algo va avoir pas mal de choses à faire. Voici les différentes étapes :
- Lecture des capteurs
- Calcul des angles & vitesses angulaires
- Lecture du récepteur radio
- Calcul des consignes
- Calcul des erreurs
- Calcul des sorties : régulateur PID
- Compensation de la chutte de batterie
- Génération des signaux de sortie
Les étapes 1, 2 & 3 ont déjà été faites dans les chapitre 6 et chapitre 7, il nous reste à implémenter le reste. Au boulot !
2.1 Calcul des consignes
Pour traduire les signaux reçu dans une dimension exploitable par le régulateur nous allons utiliser la fonction suivante :
/**
* Calcul la consigne d'un axe en degré/sec.
*
* @param float angle Angle mesuré en degré sur l'axe (X, Y, Z)
* @param int channel_pulse Durée en µs de l'impulsion reçue pour l'axe (comprise entre 1000µs et 2000µs)
* @return float
*/
float calculateSetPoint(float angle, int channel_pulse) {
float level_adjust = angle * 15;
float set_point = 0;
// On s'accorde une marge 16µs pour de meilleurs résultats
if (channel_pulse > 1508) {
set_point = channel_pulse - 1508;
} else if (channel_pulse < 1492) {
set_point = channel_pulse - 1492;
}
set_point -= level_adjust;
set_point /= 3;
return set_point;
}
Ce calcul permet d'obtenir une consigne exprimée en °/sec. On applique ce calcul pour chacun des 3 axes.
Elle sort d'où la valeur $15$ ?
Ce coefficient sert à limiter la valeur maximale de l'inclinaison du drone. Avec la valeur $15$, on obtient une inclinaison maximale de ±32.8°.
Démonstration
La fonction ci-dessus peut être exprimée par la formule suivante (pour pulse > 1508) :
$$set\_point = \dfrac{pulse-1508 - angle \times 15}{3}$$
De cette formule on extrait l'angle :
$$angle = \dfrac{-3 \times set\_point + pulse - 1508}{15}$$
Par définition, lorsque le drone a atteint la consigne, set_point vaut 0°/s. Dans ce cas, l'expression de l'angle devient :
$$angle = \dfrac{pulse - 1508}{15}$$
La valeur maximale de pulse est $2000µs$, ce qui donne alors une valeur d'angle maximale 32.8°.
Si vous voulez changer l'angle maximal, libre à vous de changer le coefficient 15 par la valeur de votre convenance.
2.2 Calul des erreurs
Maintenant que les consignes sont calculées, on peut calculer les différentes erreurs dont le régulateur PID a besoin :
/**
* Calcul des erreurs
*/
void calculateErrors() {
// Calcul des erreurs courantes
errors[YAW] = angular_motions[YAW] - pid_set_points[YAW];
errors[PITCH] = angular_motions[PITCH] - pid_set_points[PITCH];
errors[ROLL] = angular_motions[ROLL] - pid_set_points[ROLL];
// Calcul des sommes d'erreurs : composante intégrale
error_sum[YAW] += errors[YAW];
error_sum[PITCH] += errors[PITCH];
error_sum[ROLL] += errors[ROLL];
// on s'assure que ∫e.Ki ne dépasse pas 400
error_sum[YAW] = minMax(error_sum[YAW], -400/Ki[YAW], 400/Ki[YAW]);
error_sum[PITCH] = minMax(error_sum[PITCH], -400/Ki[PITCH], 400/Ki[PITCH]);
error_sum[ROLL] = minMax(error_sum[ROLL], -400/Ki[ROLL], 400/Ki[ROLL]);
// Calcul du delta erreur : composante dérivée
delta_err[YAW] = errors[YAW] - previous_error[YAW];
delta_err[PITCH] = errors[PITCH] - previous_error[PITCH];
delta_err[ROLL] = errors[ROLL] - previous_error[ROLL];
// L'erreur courante devient l'erreur précédente pour le prochain tour de boucle
previous_error[YAW] = errors[YAW];
previous_error[PITCH] = errors[PITCH];
previous_error[ROLL] = errors[ROLL];
}
2.2 Régulateur PID
On arrive maintenant au cœur des opérations !

Le but de notre régulateur PID va être de calculer la durée de l'impulsion à fournir pour chaque ESC pour agir directement sur la vitesse de rotation des moteurs.
Rappelez-vous, la durée de l'impulsion est comprise entre 1000µs et 2000µs.
On connaît la tronche d'un régulateur PID : e.Kp + ∫e.Ki + Δe.Kd, et on a tous les éléments maintenant pour effectuer ce calcul sur chacun des axes :
// PID = e.Kp + ∫e.Ki + Δe.Kd
yaw_pid = (errors[YAW] * Kp[YAW]) + (error_sum[YAW] * Ki[YAW]) + (delta_err[YAW] * Kd[YAW]);
pitch_pid = (errors[PITCH] * Kp[PITCH]) + (error_sum[PITCH] * Ki[PITCH]) + (delta_err[PITCH] * Kd[PITCH]);
roll_pid = (errors[ROLL] * Kp[ROLL]) + (error_sum[ROLL] * Ki[ROLL]) + (delta_err[ROLL] * Kd[ROLL]);
Ok super, mais ça ne nous donne pas la durée d'impulsion de chaque ESC !
Et c'est là que ça se complique.
Reprenons le schéma de notre drone et les conventions d'orientations :
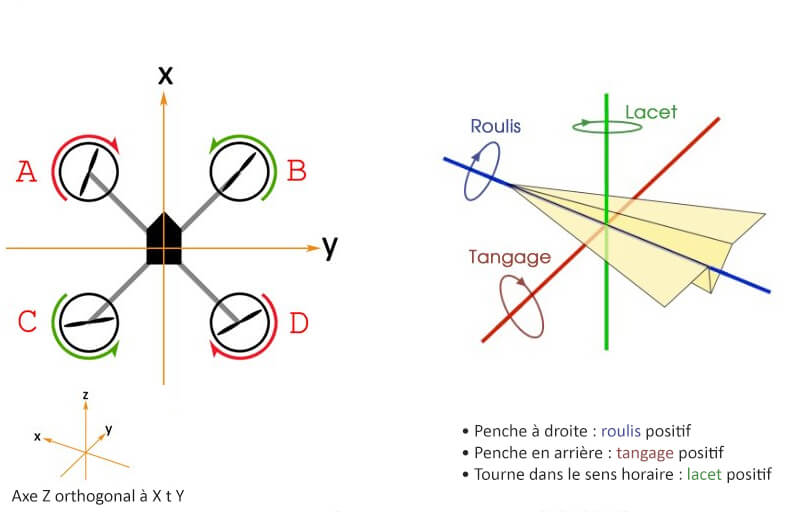
Imaginons que notre drone tourne sur son axe de roulis à +10°/s (il penche donc à droite) et que la consigne soit 0°/s.
L'erreur par rapport à la consigne est donc de $\epsilon = +10 - 0 = +10$.
Avec une erreur positive et des coefficients Kp, Ki & Kd positifs, on en déduit que $roll\_pid > 0$.
Pour redresser le drone, les moteurs A & C doivent ralentir et les moteurs B & D doivent accélérer.
Pour le moteur A par exemple, il faut donc lui soustraire $roll\_pid$ pour le faire ralentir.
| Roll (mesure) | Consigne | Erreur = mesure - consigne | roll_pid | Correction à appliquer | Opération à appliquer |
|---|---|---|---|---|---|
| +10°/s | 0°/s | +10°/s | > 0 | A & C ↘ B & D ↗ |
A -= roll_pid B += roll_pid C -= roll_pid D += roll_pid |
On applique la même logique pour l'axe pitch (tangage) :
| Pitch (mesure) | Consigne | Erreur = mesure - consigne | pitch_pid | Correction à appliquer | Opération à appliquer |
|---|---|---|---|---|---|
| +10°/s | 0°/s | +10°/s | > 0 | A & B ↘ C & D ↗ |
A -= pitch_pid B -= pitch_pid C += pitch_pid D += pitch_pid |
Et pour l'axe yaw (lacet) :
| Yaw (mesure) | Consigne | Erreur = mesure - consigne | yaw_pid | Correction à appliquer | Opération à appliquer |
|---|---|---|---|---|---|
| +10°/s | 0°/s | +10°/s | > 0 | A & D ↗ B & C ↘ |
A += yaw_pid B -= yaw_pid C -= yaw_pid D += yaw_pid |
De base, on intialise la vitesse de rotation de chaque moteur avec la valeur du throttle. Au final, en regroupant tout ça on obtient :
pulse_length_esc1 = throttle - roll_pid - pitch_pid + yaw_pid;
pulse_length_esc2 = throttle + roll_pid - pitch_pid - yaw_pid;
pulse_length_esc3 = throttle - roll_pid + pitch_pid - yaw_pid;
pulse_length_esc4 = throttle + roll_pid + pitch_pid + yaw_pid;
Et pour être sûr de ne pas se retrouver avec des valeurs complètements démesurées, on va simplement s'assurer de les conserver dans l'intervalle $[1100, 2000]_ {\mu s}$ :
pulse_length_esc1 = minMax(pulse_length_esc1, 1100, 2000);
pulse_length_esc2 = minMax(pulse_length_esc2, 1100, 2000);
pulse_length_esc3 = minMax(pulse_length_esc3, 1100, 2000);
pulse_length_esc4 = minMax(pulse_length_esc4, 1100, 2000);
J'ai mis 1100µs comme valeur min pour être sûr que les moteurs tournent au ralenti une fois le drone démarré.
2.3 Start/stop
Pour des raisons de sécurité, on va implémenter une fonction de démarrage/arrêt du drone.
Par défaut, le drone est dans l'état STOPPED. Tant qu'il est dans l'état STOPPED, on peut bouger les sticks de la radiocommande, rien ne doit se passer.
Une fois le drone dans l'état STARTED, les moteurs tournent au ralenti par défaut et le régulateur PID assure le reste.
Pour éviter un décollage chaotique, on ré-initialisera les variables du contrôleur PID à chaque passage à l'état STARTED
Les commandes seront les suivantes :
- Démarrage : bouger le stick de gauche dans le coin inférieur gauche et le ramener au centre.
- Arrêt : bouger le stick de gauche dans le coin inférieur droit.
On peut représenter cet algo par une simple machine à état :
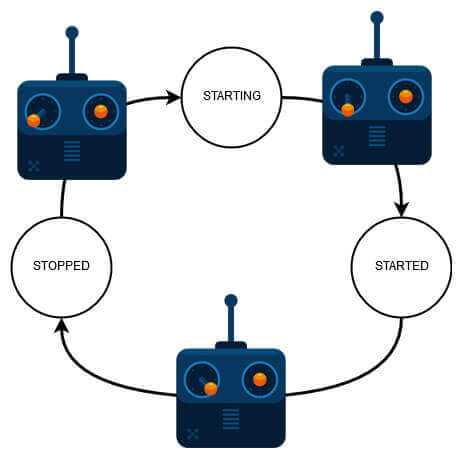
Pour ce faire, on va implémenter une fonction isStarted() qui calculera le statut du drone et retournera true s'il est STARTED :
// On declare quelques constantes pour la lisibilité
#define STOPPED 0
#define STARTING 1
#define STARTED 2
// On initialise l'état à STOPPED
int status = STOPPED;
/**
* @return bool
*/
bool isStarted()
{
// Quand le stick de gauche est positionné dans le coin inférieur gauche
if (status == STOPPED && pulse_length[mode_mapping[YAW]] <= 1012 && pulse_length[mode_mapping[THROTTLE]] <= 1012) {
status = STARTING;
}
// Quand le stick de gauche revient au centre
if (status == STARTING && pulse_length[mode_mapping[YAW]] == 1500 && pulse_length[mode_mapping[THROTTLE]] <= 1012) {
status = STARTED;
// Ré-initialise les variables du PID pour éviter un démarrage chaotique
resetPidController();
resetGyroAngles();
}
// Quand le stick de gauche est positionné dans le coin inférieur droit
if (status == STARTED && pulse_length[mode_mapping[YAW]] >= 1988 && pulse_length[mode_mapping[THROTTLE]] <= 1012) {
status = STOPPED;
// On s'assure de stopper touts les moteurs
stopAll();
}
return status == STARTED;
}
Il suffit alors de l'appeler dans loop() :
void loop()
{
// ...
if (isStarted()) {
pidController();
}
// ...
}
2.4 Compenser la baisse de batterie
Au bout d'un moment d'utilisation, la tension de la batterie va diminuer ce qui a pour conséquence directe une diminiution de la portance du drone. Pour compenser ça, il faut augmenter la vitesse de rotation des moteurs.
On va donc simplement lire la tension d'alimentation avec une entrée analogique de l'Arduino et appliquer un facteur de compensation aux moteurs.
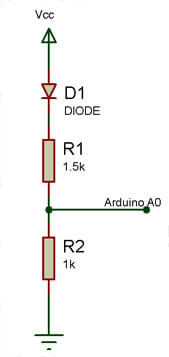
On réalise simplement un pont diviseur de tension relié à l'entrée analogique A0 de l'arduino et on ajoute ce bout de code :
// Variable globale
int battery_voltage = 0;
void loop() {
// ...
compensateBatteryDrop();
// ...
}
/**
* Compense la baisse de tension de la batterie.
*/
void compensateBatteryDrop() {
if (isBatteryConnected()) {
int coeff = ((1240 - battery_voltage) / (float) 3500);
pulse_length_esc1 += pulse_length_esc1 * coeff;
pulse_length_esc2 += pulse_length_esc2 * coeff;
pulse_length_esc3 += pulse_length_esc3 * coeff;
pulse_length_esc4 += pulse_length_esc4 * coeff;
}
}
/**
* Retourne TRUE si la batterie est bien connectée, FALSE sinon.
*/
bool isBatteryConnected() {
// On applique un simple filtre passe-bas pour filtrer le signal (Fc ≈ 10Hz et gain de ~2.5dB dans la bande passante)
battery_voltage = battery_voltage * 0.92 + (analogRead(0) + 65) * 0.09853;
return battery_voltage < 1240 && battery_voltage > 800;
}
2.5 Générer les signaux des ESC
Nous arrivons à la dernière étape : générer les signaux de contrôle des ESC.
Pourquoi on n'utilise pas simplement la librairie Servo comme pour la calibration des ESC ?
Parce que la librairie Servo ne permet de générer que des signaux d'une fréquence de 50Hz. Dans le cas de notre drone, nous avons besoin d'une fréquence de 250Hz.
Et comme nous avons déjà mis en place un timer à 250Hz pour la partie IMU (ch. 7), on va pouvoir le réutiliser pour la génération des signaux.
Comme dans le chapitre 6, nous allons manipuler les ports d'entrée/sortie pour des raisons de performances.
L'algorithme est assez simple : on passe toutes les sorties à l'état HAUT en même temps. On attend que la durée correspondante à chaque impulsion soit écoulée pour repasser la sortie concernée à l'état BAS.
Voici ce que ça donne en langage Arduino :
void applyMotorSpeed() {
// Fs = 250Hz : on envoie les impulsions toutes les 4000µs
while ((now = micros()) - loop_timer < 4000);
// Update loop timer
loop_timer = now;
// On active les broches #4 #5 #6 #7 (état HIGH)
PORTD |= B11110000;
// On boucle tant que toutes les sorties ne sont pas retournées à l'état LOW
while (PORTD >= 16) {
now = micros();
difference = now - loop_timer;
if (difference >= pulse_length_esc1) PORTD &= B11101111; // Passe la broche #4 à LOW
if (difference >= pulse_length_esc2) PORTD &= B11011111; // Passe la broche #5 à LOW
if (difference >= pulse_length_esc3) PORTD &= B10111111; // Passe la broche #6 à LOW
if (difference >= pulse_length_esc4) PORTD &= B01111111; // Passe la broche #7 à LOW
}
}
2.6 Code final
Ca y est, on en a fini avec le code !

Vous vous en doutez, avec tout ce qu'on a vu et implémenté durant cette série d'articles, le code final est volumineux. C'est pourquoi je ne vais pas l'exposer ici. Vous trouverez la version complète sur mon repo github.
Je vous rappelle que vous pouvez personnaliser le mode de votre radiocommande en éditant à votre convenance la fonction configureChannelMapping().
Pour plus d'info, je vous renvoie au chapitre 6.
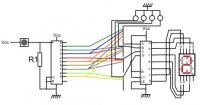
3. Cablage
Et finalement, voici comment cabler tout ce petit monde :

Vous noterez que le récepteur est alimenté par une sortie BEC d'un des ESC
4. Calibration des coefficients PID
Si votre drone a les mêmes dimensions que le miens, les coefficients par défaut devraient faire l'affaire et vous pouvez passer directement à la suite.
Sinon, il va vous falloir déterminer les valeurs des coefficients $K_p$, $K_i$ & $K_d$ pour les trois axes yaw, pitch & roll. Comme les moteurs sont organisés en carré, les coefficients des axes pitch & roll sont les mêmes. Ce qui fait 6 valeurs au total à définir.
Ces coefficients peuvent être calculés ou bien déterminé par l'expérience. Pour les calculer, ça nécessite de connaître la fonction de transfert du système à asservir, information que nous n'avons pas ici.
Nous allons donc voir la méthode par l'expérience.
4.1 Banc de test
Pour cette étape de calibration, je vous recommande grandement de vous fabriquer un banc de test sur lequel fixer le drone, comme ceci :

Ça vous évitera de flinguer votre drone en l'envoyant dans la table de la cuisine...
4.2 Procédure de calibration
1. Commencez par initialiser tous les coefficients à 0 et les coefficients de l'axe Z comme ceci :
- $K_p = 3$
- $K_i = 0.02$
- $K_d = 0$
Laxe Z n'a pas besoin de correction dérivée
2. Ensuite, augmentez la valeur de Kd (roll & pitch). Allumez les gaz jusqu'à ce que le drone commence tout juste à s'élever.
Augmentez Kd jusqu'à ce que le drone commence à osciller. Diminuez alors sa valeur jusqu'à ce que le drone redevienne stable. Dans mon cas, j'obtiens la valeur de $K_d = 20$. Diminuez cette valeur de 25% ce qui donne la valeur finale de $K_d = 15$.
3. Augmenez ensuite Kp par pas de 0.2 jusqu'à ce que le drone commence à osciller. Diminuez la valeur trouvée de 25% et vous obtenez la valeur finale de Kp. Dans mon cas je trouve $K_p = 1.3$.
4. Augmentez le gain Ki par pas de 0.01. Le drone est censé devenir de plus en plus stable. Continuez d'augmenter Ki jusqu'à ce que le drone commence à osciller lentement. Diminuez ensuite Ki de 25% ce qui vous donne sa valeur finale. Dans mon cas je trouve $K_i = 0.05$.
5. Finalement augmentez à nouveau Kp jusqu'à ce que le drone oscille rapidement. Diminuez ensuite légèrement cette valeur et vous aurez un drone stable !
Vous pouvez continuer à ajuster les coefficients jusqu'à trouver la config qui vous convient le mieux.
5. Premier vol
5.1 Sécurité & législation
Aussi cool soit le modélisme aérien, il est soumis à des règlementations. En France, il y a beaucoup de règles qu'il vaut mieux connaître si on ne veut risquer une amende ou la confiscation du matos : https://www.service-public.fr/particuliers/vosdroits/F34630
Voici 10 règles d'or à suivre pour piloter un drone de loisir :
Renseignez-vous sur la législation de votre pays avant de vous lancer dans une session de vol.
5.2 Décollage !
Le temps est arrivé d'effectuer votre tout premier vol !
Il s'agit d'un moment important et que vous attendez depuis longtemps. Alors, pour ne rien gâcher, voici quelques conseils tirés de mon expérience personnelle :
- Lunettes de protection : un drone qui se viande c'est des éclats d'hélices qui volent dans tous les sens à très grande vitesse.
J'en ai pris un dans le front (c'est pas passé loin de l'œil), ça pissait le sang, alors on se protège ! - Météo clémente : je sais que vous êtes pressé mais pas la peine de sortir s'il y a du vent ou de la pluie. Attendez qu'il fasse beau et que le vent tombe sinon, vous allez retrouver votre drone dans un arbre voir pire...
- Terrain dégagé : trouvez-vous un coin dégagé, loin des habitations et des routes. Si vous perdez le contrôle de votre drone ça vous évitera un accident grave. D'autant que les premières fois, on galère à maîtriser le bouzin
Le cas échéant, demandez la permission de squater un champ à un agriculteur le temps de votre session - Accompagnateurs : c'est toujours plus sympa de partager un moment comme ça à plusieurs. Et en cas de pépin vous ne serez pas seul.
Et puis c'est l'occasion d'immortaliser ce moment en demandant à un pote de filmer ! - Batterie : assurez-vous d'avoir rechargé vos LiPo et piles de radiocommandes. Ça serait dommage de se rendre compte sur place que les batteries sont à plat
Je ne vais pas faire un liste exhaustive mais vous voyez l'idée : safety & fun !


6. Conclusion
Tout au long de ce projet nous aurons exploré le champ des possibles de notre bon vieil Arduino Uno. C'est qu'il en a dans le bide finalement !
Il s'agit d'un sujet tout aussi passionnant que complexe donc ne vous découragez pas si ça ne marche pas du premier coup. Je vais vous révéler un secret : ça ne marche jamais du premier coup.
Persévérez, documentez-vous, parlez avec des passionnés et tout ira bien.
Vous aurez pu le sentir, le drone vol mais a quand même vite tendance à glisser sous le vent et faire du vol stationnaire est loin d'être aussi simple que ce qu'on pense !
On pourrait alors tout à fait imaginer de rajouter de nouveaux capteurs pour améliorer l'expérience de vol :
- altimètre pour garder une altitude stable (vol stationnaire)
- boussole pour garder un cap
- GPS pour garder une position (vol stationnaire)
- télémètre pour les phases de décollage/atterrissage
- ...
Ça fera peut-être l'objet de prochains articles mais rien de sûr.
D'ici là bon vol et à bientôt sur Fire-DIY !
Autres articles dans la catégorie Electronique :
Vos réactions (0) :
- Sois le/la premier(e) à commenter cet article !